Anyway I ported this code over from an nvidia CG shader demo to glsl
http://vcg.isti.cnr.it/publications/pap ... dering.pdf
Video of the code in action
https://www.youtube.com/watch?v=qAASBiVig7I
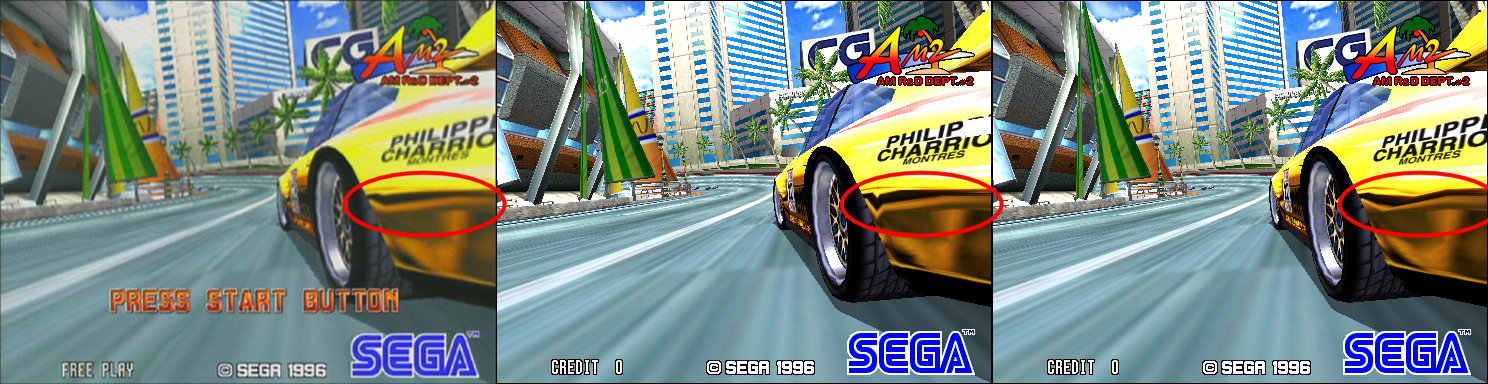
Some screenshots
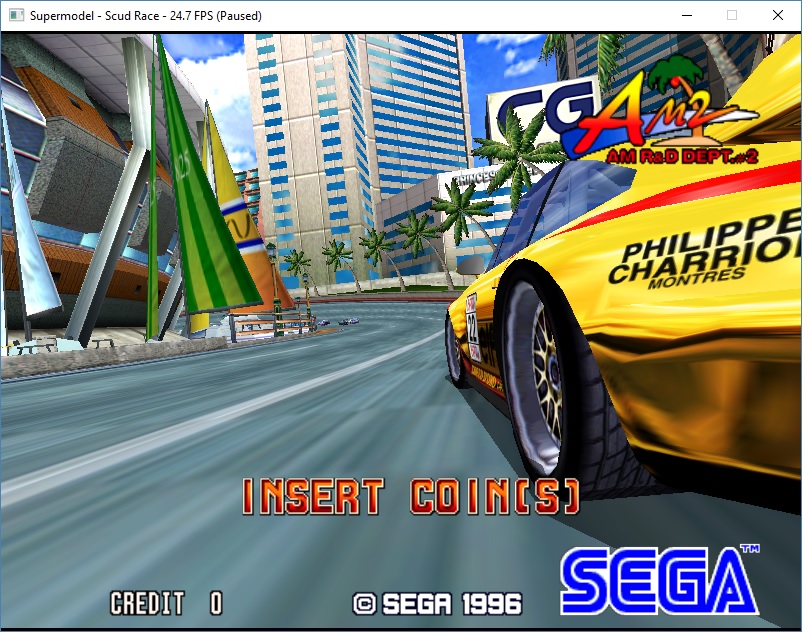
Conventional rendering (split quad into 2 triangles)
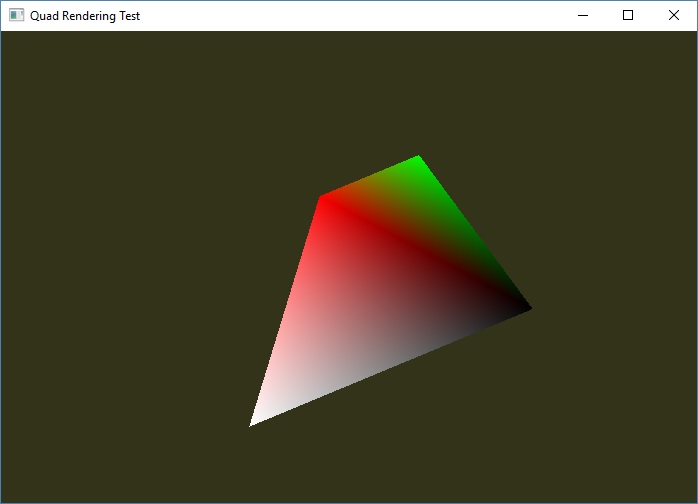
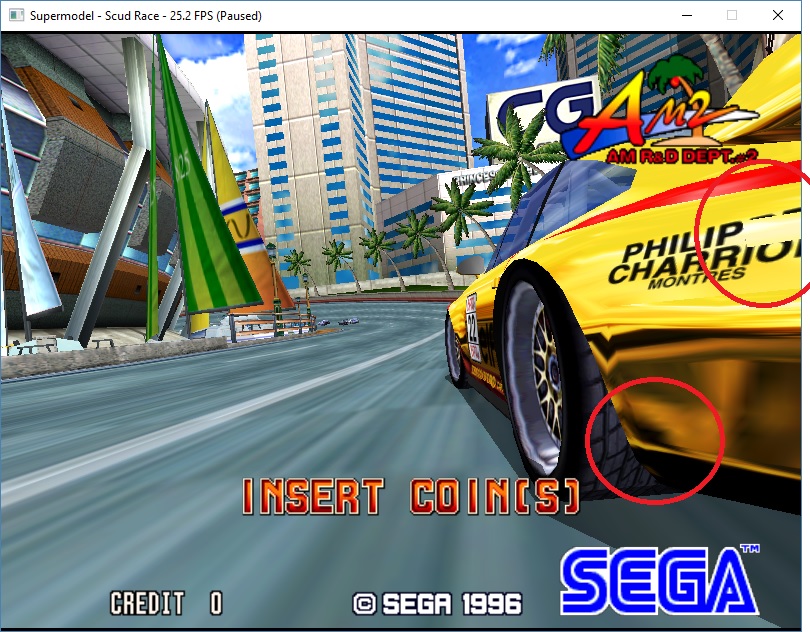
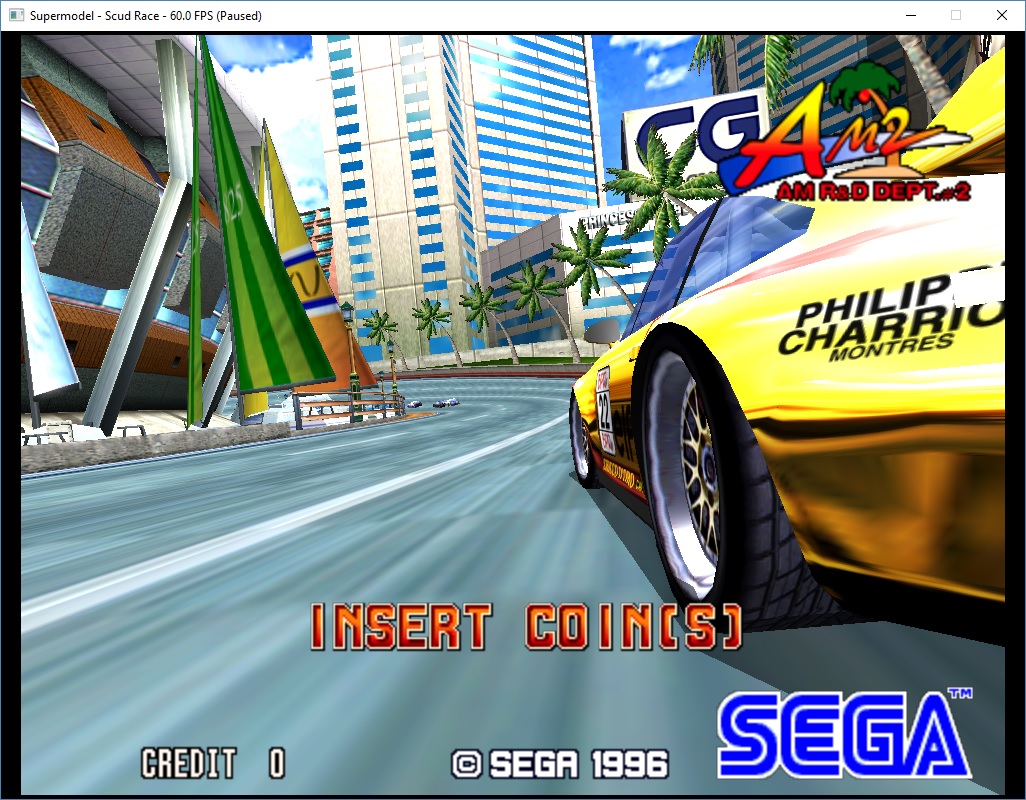
Proper quadratic emulation
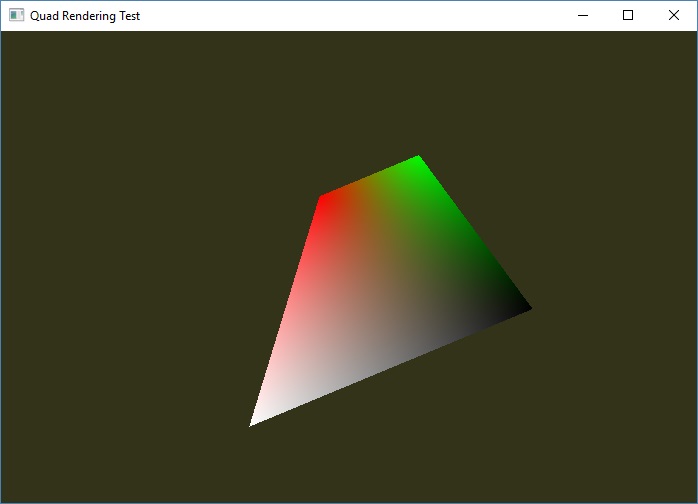
Source code
Vertex shader (yes test vertices being generated in the vertex shader)
- Code: Select all
#version 410 core
uniform mat4 mvp;
uniform mat4 modelMat;
uniform int vid_offset = 0;
out VS_OUT
{
vec4 color;
} vs_out;
void main(void)
{
const vec4 vertices[] = vec4[](vec4(-0.0, -0.5, 0.0, 1.0),
vec4( 0.5, -0.5, 0.0, 1.0),
vec4( 0.5, 0.5, 0.0, 1.0),
vec4(-0.5, 0.5, 0.0, 1.0));
const vec4 colors[] = vec4[](vec4(1.0, 0.0, 0.0, 1.0),
vec4(0.0, 1.0, 0.0, 1.0),
vec4(0.0, 0.0, 0.0, 1.0),
vec4(1.0, 1.0, 1.0, 1.0));
gl_Position = mvp * vertices[(gl_VertexID + vid_offset) % 4];
vs_out.color = colors[(gl_VertexID + vid_offset) % 4];
}
Geometry shader
- Code: Select all
#version 410 core
layout (lines_adjacency) in;
layout (triangle_strip, max_vertices = 4) out;
in VS_OUT
{
vec4 color;
} gs_in[4];
out GS_OUT
{
vec2 v[4];
float area[4];
float oneOverW[4];
vec4 color[4];
} gs_out;
float area(vec2 a, vec2 b)
{
return a.x*b.y - a.y*b.x;
}
void main(void)
{
int i, j, j_next;
vec2 v[4];
for (i=0; i<4; i++) {
float oneOverW = 1.0 / gl_in[i].gl_Position.w;
gs_out.color[i] = gs_in[i].color * oneOverW;
gs_out.oneOverW[i] = oneOverW;
v[i] = gl_in[i].gl_Position.xy * oneOverW;
}
for (i=0; i<4; i++) {
// Mapping of polygon vertex order to triangle strip vertex order.
//
// Quad (lines adjacency) Triangle strip
// vertex order: vertex order:
//
// 1----2 1----3
// | | ===> | \ |
// | | | \ |
// 0----3 0----2
//
int reorder[4] = int[]( 0, 1, 3, 2 );
int ii = reorder[i];
for (j=0; j<4; j++) {
gs_out.v[j] = v[j] - v[ii];
}
for (j=0; j<4; j++) {
j_next = (j+1) % 4;
gs_out.area[j] = area(gs_out.v[j], gs_out.v[j_next]);
}
gl_Position = gl_in[ii].gl_Position / gl_in[ii].gl_Position.w;
EmitVertex();
}
}
Fragment shader
- Code: Select all
#version 410 core
in GS_OUT
{
vec2 v[4];
float area[4];
float oneOverW[4];
vec4 color[4];
} fs_in;
out vec4 color;
vec4 GetQuadColour()
{
uint i, i_next, i_prev;
vec2 s[4];
float A[4];
for (i=0; i<4; i++) {
s[i] = fs_in.v[i];
A[i] = fs_in.area[i];
}
float D[4];
float r[4];
for (i=0; i<4; i++) {
i_next = (i+1)%4;
D[i] = dot(s[i], s[i_next]);
r[i] = length(s[i]);
if (fs_in.oneOverW[i] < 0) { // is w[i] negative?
r[i] = -r[i];
}
}
float t[4];
for (i=0; i<4; i++) {
i_next = (i+1)%4;
t[i] = (r[i]*r[i_next] - D[i]) / A[i];
}
float uSum = 0;
float u[4];
for (i=0; i<4; i++) {
i_prev = (i-1)%4;
u[i] = (t[i_prev] + t[i]) / r[i];
uSum += u[i];
}
float lambda[4];
for (i=0; i<4; i++) {
lambda[i] = u[i] / uSum;
}
/* Discard fragments when all the weights are neither all negative nor all positive. */
int lambdaSignCount = 0;
for (i=0; i<4; i++) {
if (lambda[i] < 0) {
lambdaSignCount--;
} else {
lambdaSignCount++;
}
}
if (abs(lambdaSignCount) != 4) {
discard;
}
vec4 interp_colorOverW = vec4(0.0);
float interp_oneOverW = 0;
for (i=0; i<4; i++) {
interp_colorOverW += lambda[i] * fs_in.color[i];
interp_oneOverW += lambda[i] * fs_in.oneOverW[i];
}
return interp_colorOverW / interp_oneOverW;
}
void main(void)
{
color = GetQuadColour();
}
The only thing it won't render is triangles. But we could easily emulate this being creating an imaginary 4th point out of an average of vertices 1 and 3. Then we could render everything with the same render path. The example shaders only work with colour interpolation. But it should be trivial enough to add texture coordinates and other vertex attributes.